convolve2

Convolution Integral for two dimensional data. More...

Functions
AFAPI array	convolve2 (const array &signal, const array &filter, const convMode mode=AF_CONV_DEFAULT, const convDomain domain=AF_CONV_AUTO)
	C++ Interface for convolution on two dimensional signals. More...
AFAPI array	convolve2NN (const array &signal, const array &filter, const dim4 stride, const dim4 padding, const dim4 dilation)
	C++ Interface for 2D convolution. More...
AFAPI array	fftConvolve2 (const array &signal, const array &filter, const convMode mode=AF_CONV_DEFAULT)
	C++ Interface for convolution on 2D signals using FFT. More...
AFAPI af_err	af_convolve2 (af_array *out, const af_array signal, const af_array filter, const af_conv_mode mode, af_conv_domain domain)
	C Interface for convolution on two dimensional signals. More...
AFAPI af_err	af_convolve2_nn (af_array *out, const af_array signal, const af_array filter, const unsigned stride_dims, const dim_t *strides, const unsigned padding_dims, const dim_t *paddings, const unsigned dilation_dims, const dim_t *dilations)
	C Interface for 2D convolution. More...
AFAPI af_err	af_fft_convolve2 (af_array *out, const af_array signal, const af_array filter, const af_conv_mode mode)
	C Interface for convolution on 2D signals using FFT. More...

Detailed Description

Convolution Integral for two dimensional data.

A convolution is a common operation between a source array, a, and a filter (or kernel) array b. The answer to the convolution is the same as computing the coefficients in polynomial multiplication, if a and b are the coefficients.

Another way to think about it is that the filter kernel is centered on each pixel in a, and the output for that pixel or data point is the sum of the products.

Depending on the size of the signal and the filter, any one of the following batch mode convolutions take place.

• No Batch - Single filter applied to single input.
• Filter is Batched - Many filters applied on same input
• Signal is Batched - Single filter applied to a set of inputs.
• Identical Batches - A set of filters applied onto to a set of inputs in one-to-one correspondence.
• Non overlapping Batches - All batched filters are applied to all batched signals. The batch axis of Signal and Filter should not be the same.

Note

All non-overlapping(interleaved) convolutions default to frequency domain AF_CONV_FREQ irrespective of the provided convolution mode argument.

A detailed explanation of each batch mode for 2D convolutions is provided below. Given below are definitions of variables and constants that are used to facilitate easy illustration of the operations.

• \([M\quad N]\), \([A\quad B]\) are signal, filter sizes along \(0^{th}\) & \(1^{st}\) axes respectively.
• \(P\) and \(Q\) are two constants, integers greater than one.
• \( p \) is an integer variable with range \( \ 0 \leq p < P \).
• \( q \) is an integer variable with range \( \ 0 \leq q < Q \).
• O, S and F are notations for Output, Signal and Filter respectively.

We have also used images to showcase some examples which follow the below notation.

• Each blue line is a two dimensional matrix.
• Each orange line indicates a full 2d convolution operation.
• Suffix of each letter indicates indices along \( 3^{rd}\) and \( 4^{th}\) axes in the order of appearance from left to right in the suffix.
• O, S and F are notations for Output, Signal and Filter respectively.

No Batch

Given below is an example of no batch mode.

Single 2d convolution with 2d filter

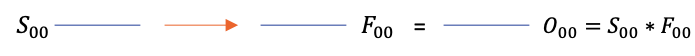
For input size \( [M \ N \ 1 \ 1] \) and filter size \( [A \ B \ 1 \ 1] \), the following set-builder notation gives a formal definition of all convolutions performed in this mode.

\( \underset{[M \ N \ 1 \ 1]}{O} \) = \( \underset{[M \ N \ 1 \ 1]}{S} \ast \underset{[A \ B \ 1 \ 1]}{F} \)

Batched Filter

Given below is an example of filter batch mode.

Single signal convolved with many filters independently

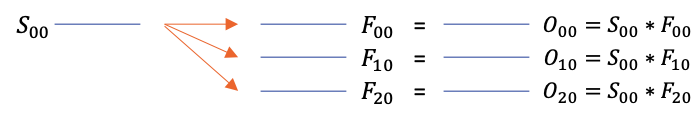
For input size \( [M \ N \ 1 \ 1] \) and filter size \( [A \ B \ P \ 1] \), the following set-builder notation gives a formal definition of all convolutions performed in this mode.

\( \underset{[M \ N \ P \ 1]}{O} \) = \( \left\{ \underset{[M \ N \ 1 \ 1]}{S} \ast \underset{[A \ B \ p \ 1]}{f} \ \Bigg\vert \ \forall \underset{[A \ B \ p \ 1]}{f} \in \underset{[A \ B \ P \ 1]}{F} \right\} \)

Batched Signal

Given below is an example of signal batch mode.

Single filter convolved with many signals independently

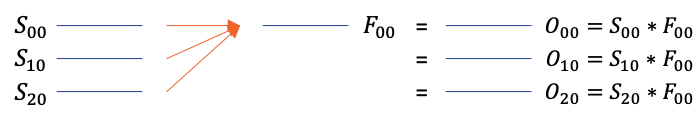
For input size \( [M \ N \ P \ 1] \) and filter size \( [A \ B \ 1 \ 1] \), the following set-builder notation gives a formal definition of all convolutions performed in this mode.

\( \underset{[M \ N \ P \ 1]}{O} \) = \( \left\{ \underset{[M \ N \ p \ 1]}{s} \ast \underset{[A \ B \ 1 \ 1]}{F} \ \Bigg\vert \ \forall \underset{[M \ N \ p \ 1]}{s} \in \underset{[M \ N \ P \ 1]}{S} \right\} \)

Identical Batch Sizes

Given below is an example of identical batch mode.

Many signals convolved with many filters in one-on-one manner

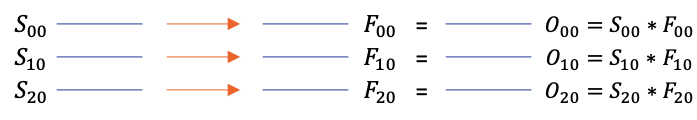
For input size \( [M \ N \ P \ Q] \) and filter size \( [A \ B \ P \ Q] \), the following set-builder notation gives a formal definition of all convolutions performed in this mode.

\( \underset{[M \ N \ P \ Q]}{O} \) = \( \left\{ \underset{[M \ N \ p \ q]}{s} \ast \underset{[A \ B \ p \ q]}{f} \ \Bigg\vert \ \forall \underset{[M \ N \ p \ q]}{s} \in \underset{[M \ N \ P \ Q]}{S} \land \forall \underset{[M \ N \ p \ q]}{f} \in \underset{[M \ N \ P \ Q]}{F} \right\} \)

Non-overlapping Batches

Four different kinds of signal and filter size combinations are handled in this batch mode. Each one of them are explained in respective sections below.

Combination 1

For input size \( [M \ N \ P \ 1] \) and filter size \( [A \ B \ 1 \ Q] \), the following set-builder notation gives a formal definition of all convolutions performed in this mode.

\( \underset{[M \ N \ P \ Q]}{O} \) = \( \left\{ \left\{ \underset{[M \ N \ p \ 1]}{s} \ast \underset{[A \ B \ 1 \ q]}{f} \ \Bigg\vert \ \forall \underset{[M \ N \ p \ 1]}{s} \in \underset{[M \ N \ P \ 1]}{S} \right\} \ \Bigg\vert \ \forall \underset{[A \ B \ 1 \ q]}{f} \in \underset{[A \ B \ 1 \ Q]}{F} \right\} \)

Given below is an example of this batch mode.

Combination 2

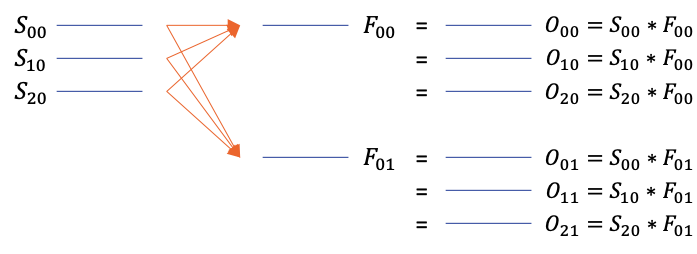
For input size \( [M \ N \ P \ 1] \) and filter size \( [A \ B \ P \ Q] \), the following set-builder notation gives a formal definition of all convolutions performed in this mode.

\( \underset{[M \ N \ P \ Q]}{O} \) = \( \left\{ \left\{ \underset{[M \ N \ p \ 1]}{s} \ast \underset{[A \ B \ p \ q]}{f} \ \Bigg\vert \ \forall \underset{[A \ B \ p \ q]}{f} \in \underset{[A \ B \ P \ Q]}{F} \right\} \ \Bigg\vert \ \forall \underset{[M \ N \ p \ 1]}{s} \in \underset{[M \ N \ P \ 1]}{S} \right\} \)

Given below is an example of this batch mode.

Combination 3

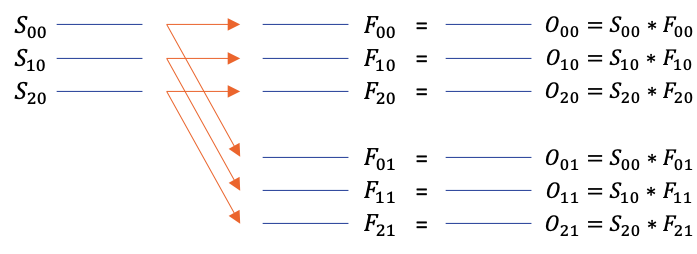
For input size \( [M \ N \ 1 \ P] \) and filter size \( [A \ B \ Q \ 1] \), the following set-builder notation gives a formal definition of all convolutions performed in this mode.

\( \underset{[M \ N \ Q \ P]}{O} \) = \( \left\{ \left\{ \underset{[M \ N \ 1 \ p]}{s} \ast \underset{[A \ B \ q \ 1]}{f} \ \Bigg\vert \ \forall \underset{[M \ N \ 1 \ p]}{s} \in \underset{[M \ N \ 1 \ P]}{S} \right\} \ \Bigg\vert \ \forall \underset{[A \ B \ q \ 1]}{f} \in \underset{[A \ B \ Q \ 1]}{F} \right\} \)

Given below is an example of this batch mode.

Combination 4

For input size \( [M \ N \ P \ Q] \) and filter size \( [A \ B \ P \ 1] \), the following set-builder notation gives a formal definition of all convolutions performed in this mode.

\( \underset{[M \ N \ P \ Q]}{O} \) = \( \left\{ \left\{ \underset{[M \ N \ p \ q]}{s} \ast \underset{[A \ B \ p \ 1]}{f} \ \Bigg\vert \ \forall \underset{[M \ N \ p \ q]}{s} \in \underset{[M \ N \ P \ Q]}{S} \right\} \ \Bigg\vert \ \forall \underset{[A \ B \ p \ 1]}{f} \in \underset{[A \ B \ P \ 1]}{F} \right\} \)

Given below is an example of this batch mode.

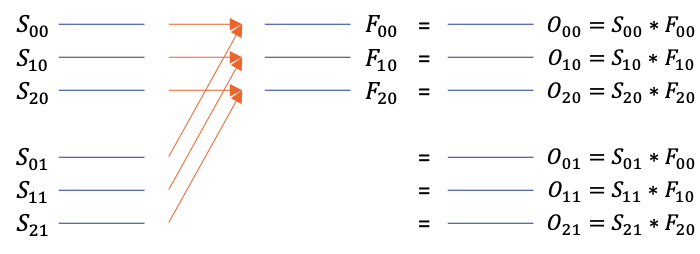
The batching behavior of convolve2NN functions(af_convolve2_nn() and af::convolve2NN() ) is different from convolve2. The new functions can perform 2D convolution on 3D signals and filters in a way that is more aligned with convolutional neural networks.

Signal Size	Filter Size	Output Size	Batch Mode	Description
\( [M \ N \ 1 \ 1] \)	\( [M \ N \ 1 \ 1] \)	\( [M \ N \ 1 \ 1] \)	No Batch	Output will be a single convolved array
\( [M \ N \ 1 \ 1] \)	\( [M \ N \ P \ 1] \)	\( [M \ N \ P \ 1] \)	Invalid	Size along second axis should be same
\( [M \ N \ P \ 1] \)	\( [M \ N \ 1 \ 1] \)	\( [M \ N \ P \ 1] \)	Invalid	Size along second axis should be same
\( [M \ N \ P \ 1] \)	\( [M \ N \ P \ 1] \)	\( [M \ N \ 1 \ 1] \)	No Batch	3D Signal and 3D filter convoled to 2D result
\( [M \ N \ P \ Qs] \)	\( [M \ N \ P \ Qf] \)	\( [M \ N \ Qf \ Qs] \)	Batch Qs * Qf	Qs signals and Qf filters to create Qs * Qf results

Note

For the above tabular illustrations, we will assume af_conv_mode is AF_CONV_DEFAULT.

Function Documentation

af_convolve2()

AFAPI af_err af_convolve2	(	af_array *	out,
		const af_array	signal,
		const af_array	filter,
		const af_conv_mode	mode,
		af_conv_domain	domain
	)

C Interface for convolution on two dimensional signals.

Parameters

[out]	out	is convolved array
[in]	signal	is the input signal
[in]	filter	is the signal that shall be flipped for the convolution operation
[in]	mode	indicates if the convolution should be expanded or not(where output size equals input)
[in]	domain	specifies if the convolution should be performed in frequency os spatial domain

Returns

AF_SUCCESS if the convolution is successful, otherwise an appropriate error code is returned.

Note

The default parameter of domain, AF_CONV_AUTO, heuristically switches between frequency and spatial domain.

af_convolve2_nn()

AFAPI af_err af_convolve2_nn	(	af_array *	out,
		const af_array	signal,
		const af_array	filter,
		const unsigned	stride_dims,
		const dim_t *	strides,
		const unsigned	padding_dims,
		const dim_t *	paddings,
		const unsigned	dilation_dims,
		const dim_t *	dilations
	)

C Interface for 2D convolution.

This version of convolution is consistent with the machine learning formulation that will spatially convolve a filter on 2-dimensions against a signal. Multiple signals and filters can be batched against each other. Furthermore, the signals and filters can be multi-dimensional however their dimensions must match.

Example: Signals with dimensions: d0 x d1 x d2 x Ns Filters with dimensions: d0 x d1 x d2 x Nf

Resulting Convolution: d0 x d1 x Nf x Ns

Parameters

[out]	out	is convolved array
[in]	signal	is the input signal
[in]	filter	is the filter that will be used for the convolution operation
[in]	stride_dims	specifies the number of stride dimension parameters
[in]	strides	array of values specifying the amounts the filter strides along each dimension
[in]	padding_dims	specifies the number of padding dimension parameters
[in]	paddings	array of values specifying the amounts to pad along each dimension
[in]	dilation_dims	specifies the number of dilation dimension parameters
[in]	dilations	array of values specifying the amounts to dilate the filter before convolving along each dimension

Returns

AF_SUCCESS if the convolution is successful, otherwise an appropriate error code is returned.

af_fft_convolve2()

AFAPI af_err af_fft_convolve2	(	af_array *	out,
		const af_array	signal,
		const af_array	filter,
		const af_conv_mode	mode
	)

C Interface for convolution on 2D signals using FFT.

Parameters

[out]	out	is convolved array
[in]	signal	is the input signal
[in]	filter	is the signal that shall be used for the convolution operation
[in]	mode	indicates if the convolution should be expanded or not(where output size equals input)

Returns

AF_SUCCESS if the convolution is successful, otherwise an appropriate error code is returned.

convolve2()

AFAPI array convolve2	(	const array &	signal,
		const array &	filter,
		const convMode	mode = AF_CONV_DEFAULT,
		const convDomain	domain = AF_CONV_AUTO
	)

C++ Interface for convolution on two dimensional signals.

    // vector<dim4> numDims;
    // vector<vector<float> > in;
    array signal(numDims[0], &(in[0].front()));
    // signal dims = [15 17 1 1]
    array filter(numDims[1], &(in[1].front()));
    // filter dims = [5 5 2 1]
 
    array output = convolve2(signal, filter, AF_CONV_DEFAULT);
    // output dims = [15 17 1 1] - same as input since expand(3rd argument is
    // false) however, notice that the 3rd dimension of filter is > 1. So, one
    // to many batch mode will be activated automatically where the 2d input
    // signal is convolved with each 2d filter and the result will written
    // corresponding slice in the output 3d array

Parameters

[in]	signal	is the input signal
[in]	filter	is the signal that shall be flipped for the convolution operation
[in]	mode	indicates if the convolution should be expanded or not(where output size equals input)
[in]	domain	specifies if the convolution should be performed in frequency os spatial domain

Returns

the convolved array

Note

The default parameter of domain, AF_CONV_AUTO, heuristically switches between frequency and spatial domain.

convolve2NN()

AFAPI array convolve2NN	(	const array &	signal,
		const array &	filter,
		const dim4	stride,
		const dim4	padding,
		const dim4	dilation
	)

C++ Interface for 2D convolution.

This version of convolution is consistent with the machine learning formulation that will spatially convolve a filter on 2-dimensions against a signal. Multiple signals and filters can be batched against each other. Furthermore, the signals and filters can be multi-dimensional however their dimensions must match.

Example: Signals with dimensions: d0 x d1 x d2 x Ns Filters with dimensions: d0 x d1 x d2 x Nf

Resulting Convolution: d0 x d1 x Nf x Ns

Parameters

[in]	signal	is the input signal
[in]	filter	is the filter that will be used for the convolution operation
[in]	stride	specifies the filter strides along each dimension
[in]	padding	specifies the padding along each dimension
[in]	dilation	specifies the amount to dilate the filter before convolution

Returns

the convolved array

Note

Make sure you pass in both dim0, and dim1 in your dim4 arguments. The third and fourth dimensions are currently ignored.

fftConvolve2()

AFAPI array fftConvolve2	(	const array &	signal,
		const array &	filter,
		const convMode	mode = AF_CONV_DEFAULT
	)

C++ Interface for convolution on 2D signals using FFT.

Parameters

[in]	signal	is the input signal
[in]	filter	is the signal that shall be used for the convolution operation
[in]	mode	indicates if the convolution should be expanded or not(where output size equals input)

Returns

the convolved array